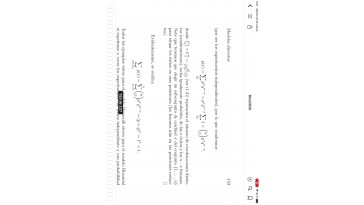
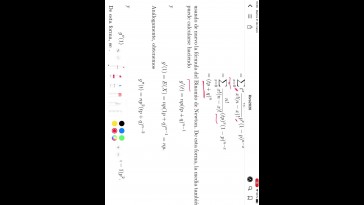
O no hicimos con el tema de modelos
discretos del tema 6,
hoy vamos a ver la instrucción,
que se denomina híper geométrica
es muy parecida.
La distribución uninominal va a
contar el número de éxitos.
La principal diferencia
es que aquí vamos a tener un
número finito de unidades,
vamos a suponer que tenemos a éxitos
fracasos y un total, a más claro
que pondremos una mayúscula.
Aquí unidad, vale?
Bueno, esta caja contenedor vamos
a sacar una muestra de tamaño,
y en esta muestra es donde
contamos de la variable
que cuenta el número de éxitos.
Cierto no quiere decir que
sea bueno sin haber
lo que se cuenta simplemente en
este caso sacar una muestra,
pues la probabilidad de
un suceso ejemplos,
y la primera que sacamos es un éxito,
la segunda, si le influye
esa probabilidad.
Por lo tanto, ya los experimentos
que son
de tipo b, pues lleno,
son independientes.
Bueno, como siempre,
lo primero que tenemos que hacer
para resolver este problema
es que ya hemos resuelto en la cual
algunos datos en particular
Valencia, y b, si queremos
hacerlo en general,
lo que tenemos que hacer es resolver
calcular cuánto vale
la función puntual de probabilidad,
que la esteriliza que abajo,
por recuerdo que es con
la probabilidad
de que haya exactamente que se éxito,
y eso lo que hacemos en la
proposición principal.
Bueno, ha ido manera de demostrarlo.
La primera por.
Dicen legisla que queráis
para Lezama.
La primera, muy parecida a
la fenomenal sentidos,
es estudiar la del binomio, que es
la que más cae en los exámenes.
Pues esta sería muy parecida para
contar el número de éxitos,
pues tenemos diversas opciones,
diversas, diversas,
reordenaciones de los
posibles éxitos.
Por ejemplo, los éxitos pueden
ir al principio
y los fracasos pueden ir al final
al hacer pruebas vale,
tendríamos todas las opciones,
que es la binomio,
pues tendríamos una unión de todas
las posibles opciones
y cómo esta unión en ti junta.
Pues esa suma, están probabilidad.
Una unión se convierte
en esta suma de aquí
en donde tenemos que contarlo,
sumandos,
y son exactamente los mismos, que
es la fenomenal sobreequipados,
y, además, todos tienen
la misma prueba.
Lo único que cambia es cómo se
calcula la probabilidad
de cada uno de los sumandos que
sería estar aquí bueno,
calculamos, con el ejemplo
en el que a los éxitos,
al principio vamos a ver, que si no,
pues también la probabilidad
de la misma.
Siempre que se mantenga fijo
el número de éxitos,
el número de fracaso en este caso
ya no son independientes,
y tenemos que usar el tema de
la probabilidad compuesta
que hizo sequía.
Entonces, la probabilidad compuesta
que nos decía que para que
ocurran estas cosas,
pues su probabilidad va a ser igual,
la probabilidad de que el
primero sea un éxito,
por la probabilidad de que
el segundo sea un éxito,
sabiendo que lo fue, primero,
y así sucesivamente, está en
la binomi, al pueblo,
no le influiría y quitábamos
esta parte
de aquí y las probabilidades
eran siempre fija.
Hace igual estapé vale, en este
caso no, y la probabilidad
de que el primero sea un éxito es
a eso los casos a favor partido
pone que son los casos totales.
Vale?
Bueno, a mí el siguiente sería a
menos -1 viniendo por enorme
nos une excesivamente hacia atrás
hasta que llegamos aquí
que justamente la probabilidad
del éxito equis,
sabiendo que los anteriores
sean éxitos
a partir de aquí ya salen fracasos.
El número de los que quedan
en sus novenos.
Si había menos equis más 1,
pues ahora hay menos y el
número de fracasos,
pues esto no ha cambiado porque
todos los anteriores han sido éxitos vale,
y así sucesivamente.
El siguiente sería uno menos
arriba y uno menos abajo,
y así hasta que llegáramos al
último, que justamente este,
para que este producto haya
exactamente en menos equis factores.
En este de aquí hay factores
y en total
allí en el por eso pasamos en
mayúscula al fenómeno.
Seguimos operando aquí con
cuidado, por ejemplo,
si necesitamos que queremos que
aparezca sobre el que tenemos
que poner el equis factorial que
aparecería aquí viviendo
y lógicamente busca que esté bien.
Hay que poner el de que factorial
afectiva, etcétera,
operando.
Aquí es fácil llegar a esta fórmula
que una vez que hemos tripliquemos
por el número de sumando,
nos va a dar la fórmula que
queríamos demostrar.
A ver si viene.
Estaré aquí vale que tradicional,
formulario que puede
llevar a Alexander
hasta esta demostración más difícil
que la segunda que vamos a ver,
pero es muy parecida a la denominada,
sea que podéis elegirla como
una manera de hacernos.
La demostración del nominal
cuando son,
depende bueno.
La segunda demostración es mucho
más corta, más sencilla,
porque directamente no
sales a formar,
pues simplemente tendríamos
que contar los casos
en los que aparecen exactamente
equis éxitos y en seguir caso,
y el número de casos totales
número de casos totales,
cuando tenemos un contenedor con
el unidades quizá acabamos
con su conjunto de tamaño viene,
pues lógicamente en sobre el número
de subconjunto de tamaño minúscula,
un tamaño de un conjunto
de tamaño mayúscula,
pues las combinaciones de elementos
tomados de nn.
Eso serían todas las
posibles muestras
que podemos sacar de ese contenido.
Ahora de esas muestras
tenemos que ver cuáles tienen
como casos a favor,
Balec, tienen equis éxitos
y elementos franjas.
Entonces ya no podemos sacar
un conjunto cualquiera,
sino que tenemos que sacar
un conjunto que va
a estar dividido en dos conjuntos,
uno va a tener que quizá éxitos
y otro va a tener menos fracaso
poniéndolos los 2,
pues obtendríamos nuestro conjunto
de tamaño con equis éxitos
y en el medio obsequis vacas
bueno, cuántos conjuntos
hay directos?
Pues muy sencillo, aquí tenemos
que vivir más,
junto a en e en conjunto,
que vienen cardinal a los éxitos
y el conjunto que tiene,
que al final ve y que tiende
a los fracasos.
Lógicamente, su conjunto de éxitos
sale de un conjunto de tamaño.
Esos conjuntos de los fracasos
salen un conjunto de tamaño.
Por eso el número de sus conjuntos
de tamaño cardinales
es a sobre el número de
conjuntos de tamaño,
claro que ve con cardinal en
menos y ahora con cada uno
de estos y cada uno de estos
me sale una opción,
vale?
Porque bueno, total será
igual al producto,
vale?
Bueno, éramos casos de que cuidamos
cuál es el soporte,
es decir, cuál es el rango en
el que se mueve la equips.
Obviamente, se sabe que el número
de lamento de la muestra,
pues tiene que ser,
tiene que estar entre
cero viene tampoco
como estaba Juan cuando es entonces
puede sobrepasara,
porque al el número de éxitos
y de que esta variedad,
que cuenca el número de éxitos y,
además el número de fracasos
en la muestra que va
a ser menos equis,
tiene que ser más pequeño
que el número total
de éxitos en la muestra vale
despejando de aquí se obtiene
que tiene que ser mayor o igual que,
en menos a decir b menos vale.
Por eso el rango que
tiene es que la e,
que iba a ser mayor, igual que 0,
pero también mayor, igual
que este número,
es decir, va a ser mayor,
igual que el máximo entre
cero ese número
y, además, pues, tiene que ser
menor igual el menor igual
que vale la otra condición,
aparece aquí la letra b
sería el máximo del mínimo.
En ella fue pactada, casi siempre,
pues las nuevas tercero, mayúscula
va hacer si hay unidad suficiente
para rellenar el la muestra
con todo éxitos,
otro fracaso.
Bueno, como siempre que hacemos
una demostración
de una función puntual,
de probabilidad,
sabemos que la suma.
En este caso desde su igual
tráeme mayúscula,
vuélvaselo, vale sustento,
y en toda la fórmula
la fórmula del injustamente dividido.
Por esto,
esta parte que aparece dividendo no
no depende de qué y, por lo tanto,
se puede sacar factor como
pasarla al otro lado
y, por lo tanto, tenemos demostradas
esta fórmula vale como consecuencia
de que la suma de las probabilidades
son, pues igual
que el modelo.
Binomio mía?
Pues esta es la orden que
tenéis en general
para calcular la función puntual de
probabilidad de perfectamente
fijaros que r no gustan
nuestra exaltación.
Si no hubiese a la anotación a
o b en vale para nosotros
en ese amor, cuidado.
Manejo porque el único modelo
en el que los parámetros que usamos
aquí no son los mismos que lo bueno
aquí tenéis un ejemplo,
no, si tenemos.
Si queremos calcular la probabilidad
de obtener dos unidades defectuosas.
Extraer una muestra de tamaño
cinco sin reemplazamiento
en un contenedor,
es decir, en unidades de las que
hay 10 defectuosas y 90,
que no decir.
Tenemos un contenedor donde
tienen defectuosas,
que lo que llamamos éxito, 90,
que no entonces sería sería.
Bueno, luego sacamos una muestra
de tamaño cinco
vale mover siempre detrás los
parámetros pasan hacer números.
En los ejemplos.
Queremos calcular la probabilidad
de que en la muestra
haya exactamente zonas defectuosas?
Pues eso sería p 2.
Ahora ya no tenemos que pensar.
Este problema se podría hacer
por combinatoria,
pero tenemos que pensar,
reconocemos que nuestra variables
una híper geométrica,
con esos parámetros que simplemente
aplicamos la fórmula o el comando,
en este caso la fórmula secta,
que tenéis en el formulario que
acabamos de demostrar,
y sustituyendo cada número
por su valor,
pues la por 10, la b por 90,
aquí aparece aquí aparece
en menos -5 menos -2,
tres tiro abajo, 110.
Bueno, haciendo esa cuenta
donde la probabilidad exacta en
erres daríais usted a que estén,
nos piden mayúsculas, que
nos pide en el mito
y lógicamente en donde se quiere
calcular la probabilidad puntual
vale?
Bueno, pues ventall verla.
Bueno, aquí se pincharían un montón
de puntos, hacen falta en tantos aquí
a los que, como diría, siento
si fracasos suficientes,
con bastaría pintarla de 0,
cinco que donde no es cero vale
yo la pintada más sí
que es porque se vea que en
el resto, 0, en este caso
más obtiene un máximo del cero
luego comparte crecimiento.
Por tanto, está cerca de la nueva.
Claro.
Bueno, como siempre, pues
se utilizará la.
La fórmula de la suma de las
probabilidades para calcular
la media de forma directa vale en
este ejemplo híper geométrica,
pues si queremos calcular la media
pues tenemos que hacer siempre suma
de qué vale.
Cuando empezamos de cero
por si hubiese algún cero
lo tenemos que quitar,
hasta deme, vale.
Si empezase minúscula, pues
no pasaría nada.
Se pondría una.
No se cambiaría su índice,
que en ese caso este número
combinatorio
tendría un número de abajo
mayor que el de arriba.
Entonces, pues simplemente se dice
por definición o por convenio
que terceros y la más grande vale.
Bueno, usando esa anotación
y haciendo como con la binomi
al pueblo objetivos
quitarla de 15.
Aquí usando el factorial que aparece
aquí me parece obvio
que hacer escritas, la
de que igual acero,
que nos vale bueno haciendo eso
lógicamente a sobre equips
a factorial partido factorial por
al menos factorial publicando,
por el que se estáis cancela,
además lo que se hace, sacara, vale,
dejarlo como a por al menos
-1 factorial ido por el que
menos suelen factorial,
y termino.
Vale.
Por qué?
Porque de esa manera aparece
un número comendador.
Vale?
Pues el segundo paso es hacer
que empieza a hacer
o la suma simplemente tomando
y igual hay que mensual.
De esa manera la y empieza en 0.
Se empezaban uno acaba,
en su vale sustituyendo
la nueva letra.
Quedaría.
Esta suma vale en donde
si queremos aplicar
la fórmula anterior, pues
ahora a su madre,
a y b sería a bapp.
Es decir, en menos un vale.
Por lo tanto, ahora tenemos que
modificar el de abajo.
Es un término que no depende de.
Vale?
Pues se puede modificar
para que nos aparezca
en vez de sobre cómo nos aparezca en
el menos -1 en menos -1 debajo
para aplicar la fórmula.
Con, lógicamente, para eso
necesitaríamos esto,
que lógicamente, pues
se puede comprobar
que en el sobre adquirido, ponerme
menos en el menos -1,
justamente porque teníamos a
Valencia la o hacia la como queráis.
Bueno, esta forma ya hemos escrito
nuestra fórmula tal cual teníamos.
Señor vale, claro que aparece.
La suma de cero hasta menos -1.
Dónde va a aparecer el máximo de a
menos -1 o en el menos -1 vale.
Aquí tendríamos al menos
un acto o al menos -1,
aquí tendríamos correspondientemente.
Entonces, esta sería la suma
de las probabilidades
en una híper geométrica, donde
van azul a menos -1.
Da igual.
Sumar un tanto.
Esta parte desaparece.
Queda siempre aumente esto,
que va a ser la media geométrica
que tenéis que forman polares.
Fijaros que se parece mucho a la
del binomio, porque tiene
por donde alguien sería la
proporción de unidades defectuosas,
que hay unos contenidos que
justamente a partir de.
Bueno el resto de características
son bastante más complicadas
de calcular hectárea.
Hemos visto que bastante también.
Difícil.
Aquí las tareas
no hay que aprenderse algunas,
estaban en el formulario,
o pues la varianza,
o el coeficiencia.
Simetría del coeficiente de gusto.
Si se han formulado y está pues
no está por supuesto.
Vale?
También las tenéis en la wikipedia,
como el vídeo de binomio.
Bueno, como ocurre en casi todos
los modelos, por ejemplo,
la función de distribución no tiene
una fórmula explícita,
por eso no están los formularios,
no hay una fórmula,
parece que vale la única
manera de calcular fe
de que, pues es sumando todas
las probabilidades,
desde cero hasta cuando
empiezan cero enorme;
si si empiezan a hacer y acceder
a no pasa nada, vale.
Bueno, en r sí que hay un comando,
excepte que hace justamente
eso, de forma automática,
de tal manera que si queremos
calcular pues la probabilidad
de que en nuestro ejemplo anterior
aparezcan dos o menos de dos
unidades defectuosas,
pues la probabilidad es 0.
99 vale que se puede hacer
con este comando en r,
o bien sumando las probabilidades
de cero de 1,
las hemos hecho antes de estas.
Habrá que hacerla con
la fórmula a mano.
Con la calcula.
Vale?
Pues manera
se pueden calcular las, la mediana
o los quanties vale,
pero ya sabéis que se hace
poniendo la letra.
Acude delante del nombre que usan
para el modelo objetivo
aparecer si queremos la mediana,
el cero cinco sería Alfa
-Valencia, pues en los cuarteles
se pondrá un cuarto cuarto, que
es la media de cuarto,
y así sucesivamente con
el Alpha que queráis,
y los parámetros del modelo
anr cuidados son a b.
Bueno, vale.
En este caso este modelo
la banda dice que es el cero porque
cero ya sobrepasa 0, 5.
Por lo tanto, con la regla
que hemos visto,
para calcular la medida nacerá
justamente el cero
la única ya hemos visto que era
la moda también pintándola.
Por último, comentaros que el
modelo híper geométrico
se parece mucho al modelo uninominal,
cuando se muestre a poco
vale concreto.
Se considera que la aproximación
es bastante buena,
que se puede aproximar la inversión
Enderica por esta vino vial.
Una dinámica de que la probabilidad
parece fija
porque muestre muy poquitas unidades
siempre que se cumpla esta regla
vale esta regla,
que lo que equivale a decir
que la muestra tamaño
de la muestra más pequeña
que el 10 por 100
de la población general
pueden estar reglada.
Tradicional formulario
también planteársela
y cuando se cumpla,
pues se puede aproximarla híper
geométrica por la binomio,
si hace falta.
Si no hace falta faltaban, mejor
siempre usaba el modelo original.
Aquí lo tenéis.
En el ejemplo que hemos visto antes
sí se muestra un cinco por 100
que menos un 10 por 100 por
lo tanto, la aproximación
debe ser buena, buena, más o menos
se entiende que tiene dos décima.
Bien, vale.
Aquí se comprueba que tanto
la binomio que sería
está claro que aquí la probabilidad
se aproximaría
por a partir de Moreno, que es el
número de éxitos partidos;
el número de unidades, que sería
un 10 por 100 vale, vale,
sería cero con a uno parece.
Aquí palidecería nuestro modelo.
Binomio nos sale 0, siete 29 el
valor exacto que hemos calculado antes
es cero siete tenemos los
dos primeros, bien 0.
Aquí fallaría cero bueno,
son siempre mejorar.
Mejoren las aproximaciones entre
las distribuciones,
que también se pueden hacer.
La f
-de dos la hemos calculado
antes exacta.
Cero 99 con la uninominal,
calculando 0.
Un perdedor arriba habría que hacer
es tantos a mano donde hacer,
o 99, 14, mientras que
haciéndoles exacto,
donde hace 99, 33, obviamente,
siempre vamos a usar exacto
y si es posible a mano,
pues también vale,
sea que solamente estaremos
la aproximación
cuando los cálculos sean
muy complicado.

![]() o pulsar la combinación de teclas Ctrl+V.
o pulsar la combinación de teclas Ctrl+V.