En este vídeo voy a intentar
aclarar algunas ideas
respecto a los supuestos del modelo
de regresión lineal en relación
con las preguntas que me habéis
hecho a través del chat.
Vamos primero a ver en qué
consiste realmente esto,
no voy a entrenar mucho en la
teoría de estadística,
sino que va a ser un
poco una una idea
en qué consiste el concepto gráfico
que tenéis aquí véis un ejemplo de
un caso en el que la temperatura
no tiene relación alguna
con la altitud.
Aquí tenemos una serie de
observatorios dibujados
y como veis, la correlación
entre altitud
y temperatura es prácticamente
nula, por lo tanto,
si y si hiciéramos un modelo
de regresión lineal,
pues obtendría pendientes,
pero el problema
es que esto pueden ser, por ejemplo,
pues todos los posibles puntos sea
esto podría ser de altitud,
temperatura,
en todos los posibles píxeles
de una capa arrastre,
evidentemente todo porque no, pero
no podéis podréis imaginar
si estos son todos los
píxeles de Esther.
Con todo lo que promete, altitud y
todos los valores de temperatura,
entonces, la cuestión es.
Nosotros realmente no tenemos
todos estos datos.
A la hora de hacer la
regresión lineal,
sino que lo que tenemos
es un muestreo,
son los datos medidos en aquellos
puntos donde hay
un observatorio meteorológico.
Pero, claro, cuál es el tema?
Qué pasaría si tenemos la suerte
de que estos que están en rojo
son nuestros puntos observatorio.
Nosotros solamente tendríamos
datos de temperatura.
En aquellos aquellos
que están en rojo
se descuenta viendo simplemente
la disposición de los puntos.
Podemos ver que el resultado
que nos darían estos datos
sería que hay una reducción de
la temperatura conforme
aumenta la actitud.
Cuando estamos viendo en el
conjunto de los datos
no, no se da esa relación.
El valor nos nos indica como de
probable que nos pase esto
como probable es que nuestros datos
nos indiquen que hay una relación,
cuando realmente no la hay, porque
hayamos tenido muy mala suerte
a la hora de demostrarlo.
Datos.
Vamos ahora a ver qué vamos a
probar diferentes muestreos
que hemos tenido un muestreo,
casualmente porque hemos tenido
muy mala suerte,
nos da un resultado que es contrario
a lo que realmente debería salir,
que es que no hay relación.
Vamos a aprobar hacer diferentes
muestreos.
Esto es estos puntos.
Son 50 puntos del total
de 500 puntos.
Los que tengo aquí hemos visto
que estos 50 puntos nos da
un resultado engañoso.
Vamos a aprobar, que no saldría
con otro haciendo diferentes,
muestre.
Si se descuenta todas estas
visualizaciones
que están saltando son muestreos
los puntos negros
o el conjunto, el punto, mejor dicho,
es siempre el mismo.
En cada una de estas diferentes
imágenes los puntos rojos
son diferentes,
de que estamos mostrando
diferentes conjuntos
de observatorios, y se
descuenta siempre.
El color, nos sale superioridad 5,
es decir, que siempre en
todos estos muestreos
estamos haciendo el resultado.
No nos diría que la pendiente
es decir,
que no tenemos relación entre
la temperatura y actitud.
B acabamos de ver un caso, no sé
si os habéis dado cuenta,
sino pasar el vídeo para atrás en
el que salía un valor inferior
a cero con 5, un 2, 5,
significa o implica
que precisamente en cinco de cada
100 muestreos aleatorios,
vamos a encontrarnos con
una, a, con un calor
y hacerlo con 5.
En definitiva, es que el valor
nos indica la probabilidad
de que si la gente cero hemos tenido
un muestreo con tan mala suerte
que el resultado del análisis
se muestre,
nos diga que es diferente de 0.
Por lo tanto, si siempre
sale muy atento,
significa que es muy probable
que realmente la pendiente
sea cero si el pelo,
muy bajo significa que
es muy probable
que la pendiente sea diferente.
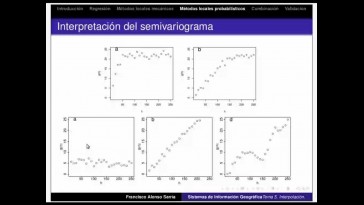
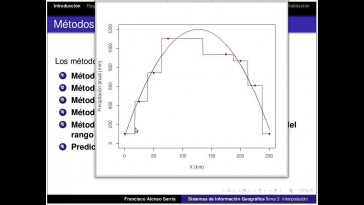
El gráfico que veis ahora nos sirve
para ilustrar la linealidad
como es.
Hay una relación clara entre
la temperatura,
pero esa relación no es lineal,
es decir los puntos no se agrupan
en torno a una línea recta,
sino que también aparece una curva
e incluso pues para el título
de bajas no parece que exista
una relación de creciente,
sino que incluso hay una
relación creciente.
Tenemos una relación entre
las variables,
pero esa relación es una línea
ocurre si intentamos movilizar esta relación
con un modelo con un modelo
de regresión lineal.
Bueno, pues que como veis no
va a salir una línea recta
en modelos en general
aparentemente bueno
tenemos pendiente negativa, tenemos
un valor muy bajo,
esa pendiente negativa pero
recuerda bastante alto
como podéis ver aquí y era
estadístico de Efe
también sabe muy bien
el error estándar
es un poquito alto, pero bueno
que podría parecer
que el modelo modelo es
bueno sin embargo
se descuenta.
Tenemos un problema porque este
error estándar que teníamos aquí
de uno con 4, nueve tres realmente
es poco representativo,
porque para algunos valores de
altitud tenemos errores,
errores positivos,
es decir estamos en estamos
estimando valores más altos que los reales aquí
y aquí mientras que en este rango
de altitudes entre 500.500
estamos estimando en general valores
de temperatura más bajos
que los que los reales.
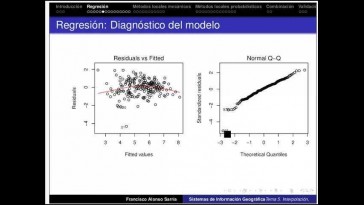
Como podíamos ver este problema en
los cuatro gráficos el diagnóstico
y el modelo bueno vamos a verlos
te quiero tenemos en cuenta
pues lo primero que aparece
aquí clarísimamente
es que la gráfico de los Valores
predichas respecto a los residuos
tiene un patrón muy claro, tienen
forma de puente de arco vale,
lo podemos encontrar
con forma de arco,
normalmente patronales con forma
de arco con forma de Hu,
y eso nos está indicando una
falta de linealidad.
Por otra parte,
si os fijáis aquí hay una, hay
una separación relativamente
de bastantes puntos respecto
a la línea correcta,
tenemos un problema de
falta de normalidad,
pero aquí el problema más grave
es la falta de calidad,
gráfica no influyentes,
porque la distancia de Google
es siempre muy, muy bien.
Vamos a ver ahora problema
vamos a ver estos datos
vienen a demostrar esa altitud,
temperatura más o menos razonables.
Como aquí simplemente viendo esta
figura ya podemos ver claramente
que hay heterogeneidad
de la variante,
pues te cuenta la temperatura
valores,
bajos de altitud es muy pequeña,
es decir, la rango de variaciones de
temperatura para la altitud baja
es muy pequeño, pero
para titular alta
como veis aquí el rango
de temperatura
es muy alto que la variabilidad
de la temperatura
es mucho mayor en estos para estas
altitudes que para estas actitudes.
Bien, cómo se va a ver esto
los cuatro gráficos?
Pues lo tenemos aquí si os
dais cuenta queremos.
Aquí vemos una forma de embudo,
vale, es la manera más clara
de distinguirlo.
Como tenemos un heterogéneo y
heterogeneidad de la alianza,
vemos que para valores estimados
bajos, es decir,
para estimar bajos, la variabilidad
de los residuos es muy alta,
mientras que para de temperatura
estimada altos los residuos
es es muy, muy baja y otra
vez se descuenta,
pues hay una pequeña divergencia
respecto a la normalidad,
mientras que por otra parte lo haré
no parece haber valores influyentes
porque no hay ningún punto de
distancia superior a cinco
vale para terminar con este libro,
vamos a ver un caso en el que
podemos ver valores influyentes.
Aquí tenemos otras veces,
otros de temperatura como en general.
La temperatura disminuye
con la altitud,
pero aquí tenemos un caso extraño,
que tenemos un caso que está
completamente al margen de los demás
y que nos da una temperatura
muy baja;
para la altitud también
bastante baja.
Esto simplemente ya no pasaría,
haría sospechar,
pero vamos a verlo otra cosa.
Antes biográfica del modelo vamos
a ver un de Regresión.
La línea negra
es la línea que tendríamos
si eliminase este punto,
si no tenemos en cuenta este punto.
No sabe esta presión que se ajusta
bastante bien al resto
de los puntos,
pero que es lo que ocurre cuando
introducimos este punto
que pesa lo suficiente.
Es lo suficientemente incluyente
como para cambiar considerablemente
la pendiente de la presión
y si os cuenta,
el las estimaciones que saldrían
con esta regresión roja,
producirían bastante más importantes
que los que se producirían
con la, con la línea.
Vamos a ver cómo podemos
o qué aspecto va a tener
este problema.
En los cuatro gráficos de
nuestro modelo vale.
Aquí si vais la a este gráfico hay
una cierta tendencia creciente
en la relación entre valores,
ajustados y residuos,
lo que suele ser un indicador de
problemas de valores influyentes
vale.
De todas maneras, es mucho más
frío, mucho más fiable.
El cuarto gráfico
que vemos que hemos un punto con
una distancia superior a 1,
vale?
Entonces, sabemos que tenemos
un punto influyente
y en este caso es mucho más
que este punto de Bale.
Entonces, estas son las cosas
que os tenéis que fijar
a la hora de hacer un diagnóstico
de un modelo de regresión,
un modelo de regresión lineal.
En estos cuatro gráficos
tenéis que buscar ver
si se cumplen la linealidad y
la hacer el primer gráfico
si se cumple la norma.
El segundo gráfico en este caso
sí porque la mayoría de los puntos
están en línea recta
aunque evidentemente que es
el valor influyente,
el punto 51 se va mucho pero el
resto están relativamente cerca de la recta
excepto algunos unos pocos,
un porcentaje muy pequeño
si la mayoría de los puntos están
cerca de la recta normalidad
y si hay muchos puntos que se alejan
de la recta significa
que no hay normalidad.
En cuanto a la heterogeneidad
de varias capas de embudo,
heterogéneo de la danza,
distribución y puntos homogéneo de la balanza
y si aparecen patrones una
una pues estaríamos
ante un problema no linealidad.
Finalmente, el cuarto nos indica
la independencia,
pero la existencia de
valores influyentes
si algún punto de este
gráfico está situado
de tal manera que tenga una
distancia superior a uno en rojo podemos decir
es un valor influyente.
Una cuestión importante
es que examen.
Si saliera un ejercicio de este tipo
y tuviera dudas podéis perfectamente
preguntarme.
Por ejemplo.
Si esto es si puedes considerar
que estos puntos están
situados en la recta
y yo contestaré sí sí o sí
no, y a partir de ahí
pues otro de los que deducir.
Lo que no me podéis preguntar
lógicamente
es si a partir de este gráfico se
puede considerar normal o no.
Vale decir si tienes dudas
respecto a así
si será un patrón no ser un patrón.
Eso lo podéis preguntar si duda,
dudas respecto a hay homogénea
o no es normal?
Eso?
Lógicamente no lo podéis preguntar.
Contexto término, estudio
que responde a un poco
de las dudas que me habéis planteado
y en uno o dos días,
con lo que lo que responde al texto
del tema de la población,
ocultar o no salir de casa.



















![]() o pulsar la combinación de teclas Ctrl+V.
o pulsar la combinación de teclas Ctrl+V.