En este vicio
voy a intentar explicaros los
métodos de interpolación local, mecánicos,
es decir, los métodos de versos
de la distancia media
ponderada por inmerso a distancia,
elevado, imponente,
método de clínex y los métodos,
y voy a empezar con los métodos de
media ponderada socialista.
Básicamente vamos a ver tres
métodos que son el método,
el vecino más próximo, más sencillo,
el método de la media, porque el
método de media ponderada,
recordar que en estos métodos
utilizados para estimar la variable
que nos interesa en el punto
de interpolación,
vamos a utilizar solamente los
puntos de muestreo más cerca
y cuántos vamos a utilizar, pues
desde los métodos mecánicos
se elige un número a priori
sin tener muy claro
si va a ser si va a funcionar mejor
o va a funcionar peor,
y podemos, por ejemplo, coger los
tres puntos más cercanas,
como en este ejemplo,
para simplificar permanente se
suelen coger más, pero bueno,
para hacer este ejemplo más
sencillo y cogido,
solamente fragmente 3.
Otra opción sería coger canalizan,
por ejemplo, cinco kilómetros,
y decir y decidir que vamos a
utilizar solamente 10 punto
demostrado que estén a menos de
cinco kilómetros del punto
de interpolación.
Bien, una vez que hemos hecho esto,
tenemos varias opciones.
El método más sencillo sería coger
simplemente el punto más cercano.
El punto de muestreo más cercana
y asignamos a este punto,
este punto donde estamos
incorporando el valor.
En el punto de muestro más cercano,
si aquí tenemos 13º, grados, pues
aquí ponemos un poquitín medio,
que pondremos 15 medio.
Es muy sencillo.
No es el método de interpretación.
Más exacto podríamos decir que
sean más inexacto de todos,
pero se ha utilizado mucho
porque se podía utilizar
antes de que hubiera de que
hubiera ordenadores
a partir de un mapa.
Podéis obtener los polígonos,
los polígonos de Thyssen,
que es en lo que se basa el método
del vecino más próximo.
Otra idea más interesante sería,
en vez de coger solamente
lo más cercano,
coger como decía antes el
punto más cercano.
Por ejemplo, tres puntos más cerca,
y calculáramos un medir.
Aquí hemos medido 13º, grados,
aquí hemos medido 15,
aquí hemos medido 17; por ejemplo,
la media sería simplemente sumar
estos tres números indiferente;
tres que nos saldría 16 vale,
por lo tanto, 16.
Por lo tanto el valor que
adjudicaría pues este punto,
el valor que estimaríamos en este
punto serían 15º grados
sentido bien, un método más
avanzado sería asumir
que es farmacológico que
esté el valor real.
En este punto se va a parecer más
al valor del punto más cercano,
es decir, todo lo que vamos a coger
para hacer la estimación,
el más parecido a este punto
más en el sistema,
cerca y el menos parecido va a
ser el que esté más lejos
entonces.
Una suposición lógica
y tenemos que ver
cómo la podemos transformar en
una ecuación matemática,
en un modelo matemático que nos
permita estimar la temperatura.
La variable que nos interese
en este punto en concreto.
Los hace haciendo en lugar de media
una media ponderada.
Si recordáis, media ponderada.
Lo que hacíamos era.
En vez de hacer en vez de sumar los
trepan directamente y entre tres
lo que hacíamos era multiplicar
cada uno de los valores.
Por un corriente de ponderación.
Es decir, que si este valor
es este 15 este 17
tenemos que guiar unos coeficientes
de ponderación
que le den más importancia
al punto más cercano
y le den menos importancia al
punto más más alejado,
para eso utilizamos esta fórmulas
que tenéis aquí
está el coeficientes de ponderación,
va a ser igual a uno partido,
por la distancia, elevado
en exponente
y es exponente generalmente, por
no decir que casi siempre, 2.
Ese inverso de la distancia elevados
se va a dividir entre la suma
de todas las inversiones,
la distancia elevados, es decir,
en el primer caso tendríamos uno
entre uno elevados que sería 1,
uno el segundo caso tendríamos
uno dividido entre dos
elevados sería, y en este caso
tendríamos uno dividido en tres
elevados, un la suma de estos tres
de estos tres números es uno con 36,
igual a uno con 36, un poco pequeña,
y lo que tendríamos que
hacer es difícil.
Cada 1.
Estos números.
Entre uno con 36 pretendíamos 1,
uno con 36, un cuarto que es,
pero como 25 entre uno
con 36 un Rodeno.
Entre 36.
Los valores que nos da
esto son 0, con 73.
Una entre pero con 73,
cero con 18.
Pero como hay 18 una,
pero vale, vale,
comprueba que la suma de estos
números es aproximadamente,
es decir, la suma de los
coeficientes de ponderación coeficientes
de ponderación va a ser igual
algo y el coeficiente
de ponderación del punto más
cercano, mucho más alto
que lo coeficientes de ponderación
de los puntos más alejados.
Por lo tanto, a la media ponderada
le estamos dando mucho más peso
al valor registrado aquí que
al valor registrador.
Vale?
Pues esto es la media ponderada, por
inversor a distancia que, bueno,
las únicas variaciones que hay
es que podemos elegir
diferente el número de puntos para
para interpolar diferente,
umbral de distancia y diferente
valor beca, error década.
De todas maneras, ya que normalmente
siempre hay dos precisamente el hecho
de que no sepamos a priori cuál
es el valor de distancia
más más adecuado en lo que
diferencia a los métodos local,
a los métodos locales mecánicos
y de los métodos locales
probabilístico método probabilístico
en el criado, hacemos el drama
precisamente para saber
cuál es la distancia más apropiada,
cuál es la distancia, umbral
más apropiada.
Intentar entender un poco mejor
el modelo de interpolación
por explosiones.
Vamos a volver un momento a
los modelos de regresión.
Aquí tenéis un ejemplo donde vemos
que hay una relación entre altitud
y temperatura, como ya dijimos
en su momento,
pero en este caso la relación
como veis,
lineal evidentemente es
un caso muy extraño,
es lo que se produjera en la
realidad, pero bueno,
si me sirve para explicarlo
lo que quiero explicar,
bueno, esto es claramente
un modelo no lineal,
como hemos dicho, pero en principio
podríamos intentar hacer un modelo
y podemos intentar utilizar
un modelo de revisión lineal,
interpolación.
Si lo hiciéramos obtendríamos si
esta línea vale como modelo,
recordar como modelo lineales,
temperaturas igual a veces
de uno o altitud.
En este caso, y vemos que el
único medio que nos sale
sería un 2, dos con 21.
Este error se calcula como la media
de los, los errores ha cuadrado
los residuos al cuadrado.
Es decir, a punto que regulamos la
diferencia entre el valor real
del barrio estimado, en este caso
sería esta diferencia.
En este caso sería esta
diferencia, etc.
Pues todos esos valores a cuadrado
calculamos la media y a esa media
le calculamos la raíz cuadra,
sí si quiere ver los resultados
del modelo,
el sumari del modelo.
No tenemos aquí.
Pues en principio nos sale
una pendiente negativa,
como era de esperar, con
un valor muy alto,
un residuo, un perdón,
un error típico,
bastante, pero bueno, dentro
de lo razonable
y un grado de 60.
Si estamos aplicando el 66 con
siete por 100 de la crianza
con el modelo, lo que significa
que, en principio el modelo,
pues no es, no parece del todo malo.
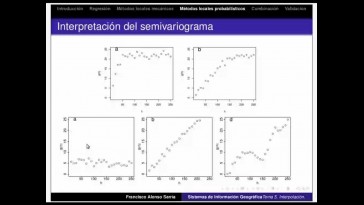
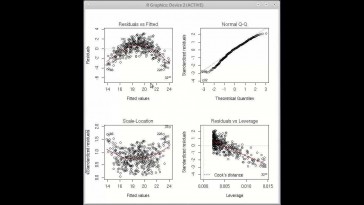
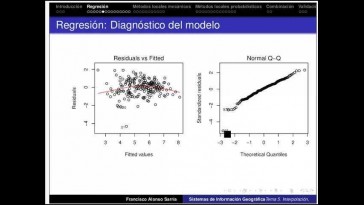
Si miramos los gráficos, así
nos vamos a dar cuenta
de que el primer gráfico se muestra
un patrón muy claro,
vale?
Eso significa que hay un
problema, pero bueno,
es algo que ya sabíamos desde el
principio viendo los datos.
Si recordáis,
cuando dije que cuando hubiera
un problema en ordinalidad
podíamos utilizar otros métodos,
uno de esos métodos podría ser,
por ejemplo, revisión,
revisión económica podría consistir
en ajustar un una parábola.
Un modelo práctico es una
fábula, sólo debería,
y si en el instituto la
eso y este modelo
tiene esta ecuación crea
temperaturas igual a la vez,
pero más de uno por la elevación
han vez dos
por la elevación al cuadro,
vale siempre 40,
se ajusta bastante mejor a
contactos y de hecho,
pues el error que dio
bajaba a la mitad.
Vale?
Cuenta igual que digamos que el
modelo lineal no se ajusta,
porque porque quedaban había
diferencias importante,
y además están diferencias
e agrupaban,
algunos valores de altitud, grados,
en el caso del modelo cuadrática,
pasa un poco lo mismo.
Entonces, cómo podríamos
intentar solucionarlo?
Bueno, pues viendo un paso,
más allá de utilizar
un modelo cuadra,
utilizaremos un modelo cúbico
modelo cúbico.
Consiste en que vamos a esta central.
Tenéis?
Como veis, este modelo se
ajusta bastante mejor
y hemos un medio 17.
Volvemos lo hemos bajado bastante en
relación con el modelo de clínex.
Lo importante tener en cuenta
es que como veis un modelo cúbico
funciona mejor que un modelo ético,
un modelo lineal, y siempre
es un modelo flexibles
para poder adaptar mejor a la
variabilidad que queremos,
que queremos analizar bien en qué
consistía, el modelo de clínex
en una sola mención como
tenemos aquí.
El modelo de doctrinas,
en una dimensión consistiría
ajustar, cubica,
has pero no para todos los
puntos al mismo tiempo,
sino solamente en algunos
rango de los puntos.
Un primer rango ajustaríamos una,
una cúbica para otro rango
ajustaríamos,
una cúbica diferente rango,
ajustaríamos, una cúbica diferente,
etc. Y el método de expiren nos
permiten también conseguir
que haya una cierta suave
en la transición de una de las
púbicas a otra de las críticas
y vamos a ver un ejemplo de cómo
quedaría, pero tenéis aquí
a quien magenta sus cuentas, no
muy diferentes de la cúbica,
porque la cúbica ubicaría era
un modelo bastante bueno,
pero aquí se descuenta la cuenca,
se iba un poco, demasiado
hacia arriba
y el modelo ha conseguido
ajustar mejor.
Esto, a base de que, bueno, pues
a base de estos datos
los estamos ajustando
solamente mismos.
Este este trozo de la curva recular.
Vamos solamente con estos puntos,
mientras que este trozo del acuerdo
está calculado con estos puntos,
sobre la curva, con estos
puntos, etcétera,
como si hubiéramos hecho, hubiéramos
cogido la lge equis,
lo hubiéramos dividido en trocitos,
y cada trozo lo hemos ajustado
con una cúbica diferente,
vale.
El procedimiento de bienes
es que él mismo se encarga de
analizar cuántos puntos de corte
hay que coger y cuál es
la redistribución.
de puntos de corte, y se
descuenta el medio,
pues hemos conseguido
bajarlo bastante.
En qué consiste entonces el método
de quienes en dos dimensiones bueno,
vamos a este ejemplo donde tenemos
con datos inventados,
un la coordenada equis,
la coordinada y valores
de temperatura,
supuestamente una serie
de observatorios,
y que lo veis aquí con un círculo.
Proporcionar a la temperatura bien,
exploración clínex sería hacer,
como hemos visto antes en vez
de en un solo con un solo
dejé con dos ejes en vez de dividir
en una serie de regiones
lo que haremos será dividir
este cuadro,
dado este territorio, en una
serie de regiones vale.
En estas regiones, Interpol,
vemos un modelo
de un modelo, despliegues, perdón,
regiones interpueblos.
Vemos una y otra cuestión.
Hay que tener en cuenta que cuando
vemos en dos dimensiones
la cúbica se complica bastante,
porque tenemos solamente los
métodos, los perdón,
no tenemos solamente los términos
que se refieren a equis,
sino que tenemos los términos que
se refieren ahí y términos
de interacción entre entre,
quise y debemos tener
en una situación de bastante
más complejas,
pero realmente da igual porque
esto lo va a hacer.
Al final el ordenador,
la idea básica es que vamos a
dividir en una serie de regiones,
en estas regiones calibraremos
un modelo de este tipo
y.
Al final la acciones se consigue
más de unas de una regiones,
a otra de manera se minimicen
los saltos.
Aunque ya lo dije en la otra en
la presentación puede ocurrir
que en algunos casos y que aparezcan,
lo que se llama sutil es decir
que dos en la zona donde es
donde se ponen dos modelos
diferentes,
ubican diferentes puede dar un salto,
un salto importante.
Vale?
Sí si vemos el resultado de hacerme
interpolación por expedientes
en estos en estos datos,
pues veremos.
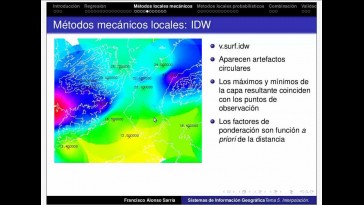
Vemos que tiene un resultado
aparentemente bastante bueno;
la temperatura es más baja en la
zona donde debe ser más baja
y donde debe ser más alta
no se produce en artefacto
circulares;
vale;
aunque en realidad todo esto
es un círculo lo podíamos;
podíamos decir un círculo,
pero se producen círculos en torno
a los puntos de muestreo,
que es el problema que ocurre
con los métodos de medias
ponderadas, basados en inversores
de distancia;
de hecho se suelen exprime;
ese es el mejor de los de
interpretación local,
el más exacto con diferencia y ya
a pues sí es el mejor o no;
pues está un poco sujeto a debate
y muchas veces del tipo
de datos que estemos manejando.
Vamos a ver ahora en qué consiste
el método de thing.
Para interpolar tenemos
los mismos puntos
que hemos visto antes.
Si recordáis,
y a partir de esos puntos de
muestreo puntos en rojo
hemos generado la red de irregular
deberían cuenta.
Tenemos varios ángulos, cada
uno de esos pueblos
se han generado uniendo
diferentes puntos de,
demuestre triángulo.
Sería excelente, vale?
Hay una serie de criterios a la
hora de opción y en general,
se trata de que queden lo
más equilátero posible,
sean, se parezcan lo máximo
posible a un triángulo
para los lados igual que obviamente
esto no siempre,
siempre va a poder ser así y por eso
telemadrid rendirse rurales
-ángulos, con triángulos diferentes
de diferentes formas.
La idea básica de todas
maneras es que
cuando nosotros queramos interpolar
por ejemplo este punto
lo que tenemos,
lo que tenemos que tener en cuenta
es dentro del triángulo.
Está el punto, vale?
Punto estaba, dentro del triángulo.
Por lo tanto lo que vamos a hacer
es tener en cuenta los los
valores observatorios.
Los puntos de muestre que
forman los vértices,
vale?
Antes hemos visto que o antes
hemos dicho hablar
de métodos de poder que aquí
teníamos federados aquí federados,
y aquí 17, también vimos
que esta distancia
eran tres kilómetros de distancia,
dos kilómetros.
Por último, está distancia.
Vale, bueno, pues ahora
lo que podemos hacer
es una media ponderada
por la distancia,
pero lo que se suele hacer
cuando utilizan útil
es una media distancia, pero lo
utilizando como eficiente,
como política, un sin elevar ninguno
de los de los términos.
De esa manera vamos a
tener qué punto.
Ponderación es uno partido
seguro que si bueno,
para el segundo punto.
Y para el tercer punto.
La suma de estos tres números
va a ser 1, 83,
por lo tanto de consideración será
uno partido, porque uno con 83,
pero con cinco.
Pido por uno con 83 pero el
33 partido por uno con 83
esto es igual a.
Con 55.
Pero con 27.
0.
Qué de nuevos humano y esto,
señores de ponderación,
que utilizaremos para resolver
esta media ponderada
a partir de estos valores,
dentro de lo que es el método
de interpolación?
Portin, vale.
Si os dais cuenta cuanto más
altos señales ética
en el caso anterior heredado,
sin suelo,
cuanto más altos el política malva
que sea la diferencia de distancia
entre unos.
Con esto termino en el vídeo de
métodos de interpolación local
pero que se haya, pido que lo
mejor de todas maneras,
como lo voy a publicar
esta misma tarde
o el lunes mañana la sesión de chat
de la sesión de prácticas.
Si tenéis alguna duda,
me lo planteáis
y no me ha dicho nada respecto
al método de criado,
mañana también nos preguntáis, qué
problemas tenéis y hacemos otro
para resolverlo?
Cómo lo hacemos?
Hasta luego el cuidados



















![]() o pulsar la combinación de teclas Ctrl+V.
o pulsar la combinación de teclas Ctrl+V.